The images above represent the output of an 8x8 matrix of simple integrate-and-fire oscillators (64 total), similar to neurons. The top image shows the output of each oscillator and the bottom scrolling graph shows the number of oscillators that have fired in each frame period. When free running they have waveforms like those on the left side of this diagram:

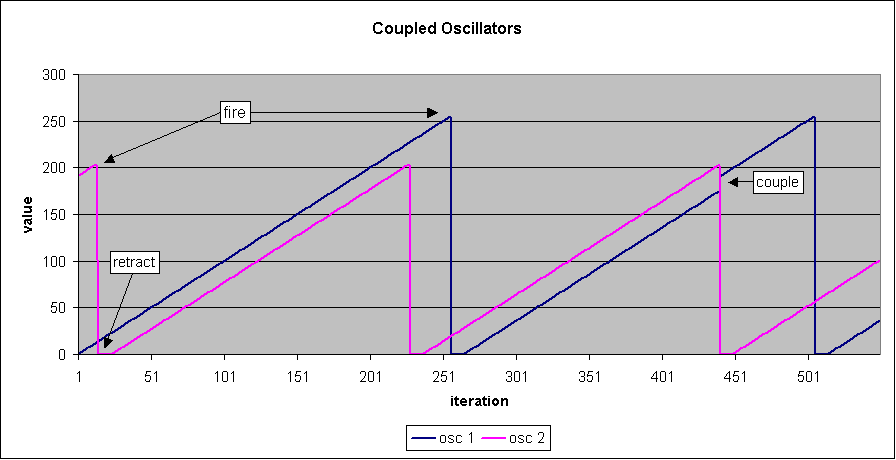
This shows the behavior of two independent oscillators which ramp up at a constant rate to a predetermined level where they fire, at which time we see a blue square flash in the panel at the top of this page. After firing they reset and wait for a retraction period before starting to ramp again.

Oscillators can be coupled to their eight immediate neighbors -- in a box around each matrix element, wrapping around on all the edges -- such that when one fires the neighbors become more likely to fire. The right hand waveform shows the effect of osc2 (in pink) firing and "bumping" osc1 up a bit so that it will fire earlier than expected. Coupling signals received during a retraction period are ignored, otherwise they contribute to the ramping of the target oscillator.

When the system starts the oscillators are set to a range of firing values within 20% of each other and to an arbitrary starting value so the phase and frequency of the initial system is entirely random. But with sufficient coupling the individuals manage to synchronize as a group. This can be seen in the lower graph as a progression from random noise to discrete regular pulses.

The controls and variable settings are:

• Random button -- Resets the system with a new set of random oscillators.


• Sync button -- Forces all the oscillators to fire at once.


• Disrupt button -- Forces nine oscillators in the middle of the frame to fire.


• Frame Time -- The number of milliseconds between matrix updates and frame displays. Each oscillator has a cycle between 204-255 frames. At 10ms the full cycle takes around 2.5 seconds but video displays may not work well. The range is clamped between 10-1000.


• Coupling Strength -- The number of counts added to the neighbors' accumulators when an oscillator fires. When set to 0 this is just a free running system. When set to a large value the system synchronizes immediately. The range is clamped between 0.0-50.0, i.e., 0-20%.


• Retraction Count -- The number of frames an oscillator is inhibited from coupling after its output fires. Coupling Strength and Retraction Count interact to make the system more or less sensitive to perturbations. The range is clamped between 0-10.

Note that some of the effects may be artifacts of updating the matrix sequentially from left to right and top to bottom, rather than completely independently.

This work was inspired by the book Sync by Steven Strogatz. To see how this might map to real biological systems see the Mirollo & Strogatz paper: Synchronization of Pulse-Coupled Biological Oscillators.